Determinan Matriks
Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau  . Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
Untuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
. Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
Untuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
Determinan Matriks Ordo 2 x 2
Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
Nilai determinan A disimbolkan dengan  , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
Contoh Soal:
Tentukan nilai determinan matriks
Pembahasan:
Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.
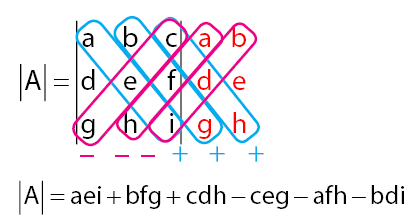
Contoh perhitungan determinan pada matriks ordo 3:
Maka,
Determinan Matriks Ordo 2 x 2
Contoh Soal:
Tentukan nilai determinan matriks
Determinan Matriks Ordo 3 x 3
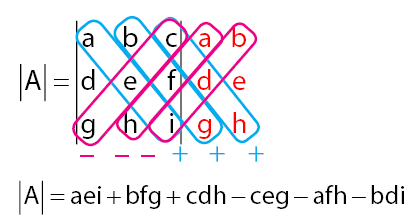
Contoh perhitungan determinan pada matriks ordo 3:
Determinan Matriks 3×3 Metode Ekspansi Kofaktor
Minor
Kofaktor
Ekspansi Baris
Satu Elemen Nol
Dua Elemen Nol
Tiga elemen nol
Ekspansi Kolom
Satu Elemen Nol
Dua elemen nol
Tiga elemen nol
Metode Cino
Sekian materi yang sedikitnya dari saya Terimakasih telah mengunjungi blog saya apabila ada kesalahan dalam materi maupun kata Mohon dimaafkan
Sekian materi yang sedikitnya dari saya Terimakasih telah mengunjungi blog saya apabila ada kesalahan dalam materi maupun kata Mohon dimaafkan











