PENJELASAN BESERTA CONTOH PERKALIAN MATRIK ~ Aljabar Linier (Smstr 1)

Pengertian Matriks

Matriks adalah kumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya dan di dalam suatu tanda kurung. Bilangan-bilangan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks. Matriks digunakan untuk menyederhanakan penyampaian data, sehingga mudah untuk diolah.

Contoh kolom dan baris pada matriks

Perhatikan perbedaan dua buah matriks yang dapat dikalikan dan dua buah matriks yang tidak dapat dikalikan pada contoh yang diberikan di bawah.

Contoh dua matriks yang tidak dapat dikalikan

kriteria matriks yang tidak dapat dikalikan

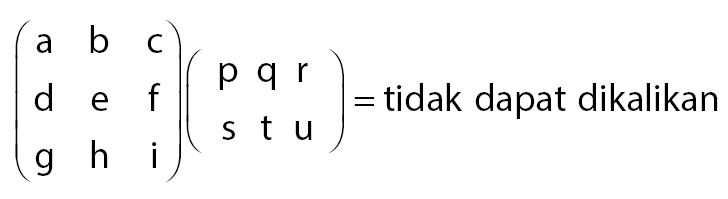
Matriks pertama mempunyai jumlah kolom sebanyak 3 dan matriks ke dua mempunyai jumlah baris sebanyak 2. Karena jumlah kolom pada matriks pertama tidak sama dengan jumlah baris pada kolom ke dua maka dua buah matriks tersebut tidak dapat dikalikan.

Contoh dua matriks yang dapat dikalikan

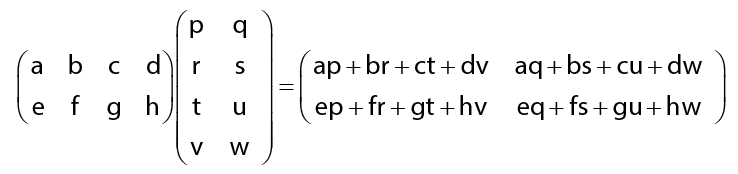
Matriks pertama pada contoh yang diberikan di atas memiliki jumlah kolom sebanyak 4 (empat) dan jumlah baris pada matriks ke dua adalah 4 (empat). Jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks ke dua. Hasil perkalia dua buah matriks ini adalah matriks dengan ukuran 2 x 2.

Selanjutnya, simak perkalian matriks yang akan diberikan lebih detail pada pembahasan di bawah. Ulasan yang pertama adalah perkalian matriks 2 x 2.

Perkalian Matriks 2 x 2

Perkalian dua buah matriks di mana kedua matriks tersebut masing-masing memiliki ukuran 2 x 2 akan menghasilkan matriks dengan ukuran 2 x 2 juga. Proses perkalian matriks ini tidak begitu rumit, hal ini dikarenakan anggota-anggota penyusun matriks dengan ukuran 2 x 2 hanya terdiri atas 4 anggota untuk setiap matriks. Sehingga, perkaliannya dapat dengan mudah dilakukan dengan tingkat kerumitan yang rendah.

Cara mengalikan dua buah matriks adalah mengalikan antar baris dan kolom. Penjelasan perkalian matriks 2 x 2 dalam gambar dapat dilihat seperti berikut.

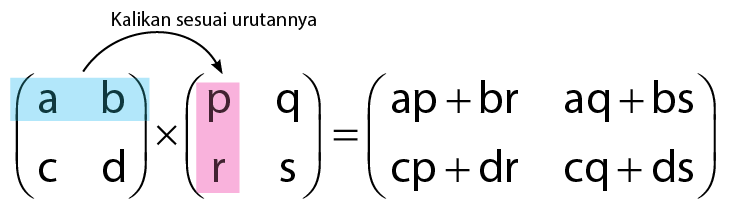
Contoh soal perkalian matriks 2 x 2

Tentukan hasil perkalian matriks A dan B di bawah!

$A = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix}$

$B = \begin{pmatrix} 7 & 5 \\ 6 & 4 \end{pmatrix}$

Jawab:

$A \times B = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 7 & 5 \\ 6 & 4 \end{pmatrix}$

$= \begin{pmatrix} 3 \cdot 7 + 4 \cdot 6 & 3 \cdot 5 + 4 \cdot 4 \\ 1 \cdot 7 + 2 \cdot 6 & 1 \cdot 5 + 2 \cdot 4 \end{pmatrix}$

$= \begin{pmatrix} 21 + 24 & 15 + 16 \\ 7 + 12 & 5 + 8 \end{pmatrix}$

$= \begin{pmatrix} 45 & 31 \\ 19 & 13 \end{pmatrix}$

Demikian, proses perkalian matriks antara dua buah matriks dengan ukuran 2 x 2. Mudah bukan? Selanjutnya simak perkalian matriks 3 x 3.

Perkalian Matriks 3 x 3

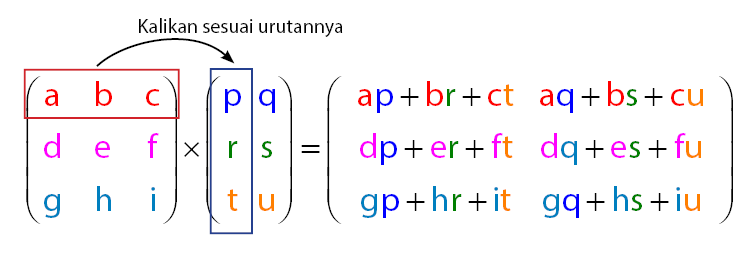
Perkalian matriks 3 x 3 sedikit lebih rumit dari perkalian matriks 2 x 2. Hal ini dikarenakan ukuran matriks 3 x 3 mempunyai jumlah anggota lebih banyak. Matriks persegi dengan ukuran 3 x 3 memiliki 9 anggota, yang terbagi dalam 3 baris dan 3 kolom. Pada matriks dengan ukuran 3 x 3, setiap baris dan kolom terdiri atas 3 anggota. Konsep perkalian pada matriks dengan ukuran 3 x 3 sama dengan proses perkalian matriks dengan ukuran 2 x 2, hanya saja lebih rumit.

Perhatikan proses perkalian dua buah matriks yang masing-masing berukuran 3 x 3 pada gambar di bawah.

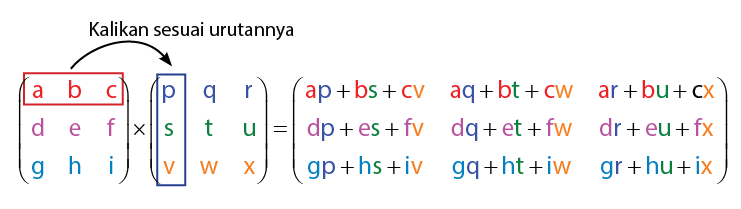
Apakah gambar di atas sudah cukup membuat jelas ? Jika belum jelas dapat disimah contoh soal perkalian matriks 3 x 3 berikut untuk menambah pemahaman kalian.

Contoh soal perkalian matriks 3 x 3

Tentukan hasil perkalian matriks 3 x 3 di bawah!

$A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$

$B = \begin{pmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{pmatrix}$

Jawab:

$A \times B = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \times \begin{pmatrix} 9 & 8 & 7 \\ 6 & 5 & 4 \\ 3 & 2 & 1 \end{pmatrix}$

$= \begin{pmatrix} 1 \cdot 9 + 2 \cdot 6 + 3 \cdot 3 & 1 \cdot 8 + 2 \cdot 5 + 3 \cdot 2 & 1 \cdot 7 + 2 \cdot 4 + 3 \cdot 1 \\ 4 \cdot 9 + 5 \cdot 6 + 6 \cdot 3 & 4 \cdot 8 + 5 \cdot 5 + 6 \cdot 2 & 4 \cdot 7 + 5 \cdot 4 + 6 \cdot 1 \\ 7 \cdot 9 + 8 \cdot 6 + 9 \cdot 3 & 7 \cdot 8 + 8 \cdot 5 + 9 \cdot 2 & 7 \cdot 7 + 8 \cdot 4 + 9 \cdot 1 \end{pmatrix}$

$= \begin{pmatrix} 9 + 12 + 9 & 8 + 10 + 6 & 7 + 8 + 3 \\ 36 + 30 + 18 & 32 + 25 + 12 & 28 + 20 + 6 \\ 63 + 48 + 27 & 56 + 40 + 18 & 49 + 32 + 9 \end{pmatrix}$

$= \begin{pmatrix} 30 & 24 & 18 \\ 84 & 69 & 54 \\ 138 & 114 & 90 \end{pmatrix}$

Perkalian Matriks (m x n) x (n x p)

Ulasan terakhir yang akan dibahas melalui halaman ini adalah perkalian dua matriks dengan ukuran berbeda. Konsep perkalian matriks masih sama dengan dua pembahasan sebelumnya, yaitu mengalikan antar elemen-elemen matriks pada baris dan kolom. Sebagai contoh, akan diulas perkalian matriks dengan ukuran 3 x 2 dan matriks dengan ukuran 3 x 2.

Perhatikan proses perkalian dua buah matriks yang masing-masing berukuran (3 x 3) x (3 x 2) pada gambar di bawah.

Contoh soal perkalian matriks (3 x 3) x (3 x 2)

$A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$

$B = \begin{pmatrix} 6 & 5 \\ 4 & 3 \\ 2 & 1 \end{pmatrix}$

Jawab:

$A \times B = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \times \begin{pmatrix} 6 & 5 \\ 4 & 3 \\ 2 & 1 \end{pmatrix}$

$= \begin{pmatrix} 1 \cdot 6 + 2 \cdot 4 + 3 \cdot 2 & 1 \cdot 5 + 2 \cdot 3 + 3 \cdot 1 \\ 4 \cdot 6 + 5 \cdot 4 + 6 \cdot 2 & 4 \cdot 5 + 5 \cdot 3 + 6 \cdot 1 \\ 7 \cdot 6 + 8 \cdot 4 + 9 \cdot 2 & 7 \cdot 5 + 8 \cdot 3 + 9 \cdot 1 \end{pmatrix}$

$= \begin{pmatrix} 6 + 8 + 6 & 5 + 6 + 3 \\ 24 + 20 + 12 & 20 + 15 + 6 \\ 42 + 32 + 18 & 35 + 24 + 9 \end{pmatrix}$

$=\begin{pmatrix} 20 & 14 \\ 56 & 41 \\ 92 & 68 \end{pmatrix}$

Demikian proses perkalian matriks 3 x 3 dengan 3 x 2, diperoleh matriks dengan ukuran 3 x 2

Sekian pembahasan perkalian matriks 3 x 3, perkalian matriks 2 x 2, dan perkalian matriks (m x n) x (n x m). Terimakasih telah mengunjungi blog saya apabila ada kesalahan dalam materi maupun kata Mohon dimaafkan

Aljabar Linier (Smstr 1)

Rabu, 18 September 2019